Answer:
(a) 774.529 kJ/kg
(b) Approximately 61.2%
(c) 96.816 kPa
(d) The maximum in the cycle temperature is 2655.3 K
Step-by-step explanation:
(a)The temperature T₂ = T₁ × r^(k - 1)
∴ T₂ = 300 × 9^(1.4 - 1) = 772.467 K
P₂ = P₁×r×T₂/T₁ = 100 × 8 × 772.467/300 = 2059.912 kPa
W₁₂ = Cv × (T₁ - T₂) = 0.717*(300 - 772.467) ≈ -338.76 kJ/kg
The heat added = q₂₃ = 1350 kJ/kg = Cv × (T₃ - T₂) = 0.717*(T₃- 772.467)
1350/0.717 = T₃- 772.467
T₃ = 1350/0.717 + 772.467 = 2655.3 K
T₄ = T₃ × (1/r)^(k - 1) = 2655.3 × (1/9)^(1.4 - 1) = 1102.596 K
W₃₄ = Cv×(T₃ - T₄) = 0.717 × (2655.3 - 1102.596) ≈ 1113.289 kJ/kg
The net work = W₁₂ + W₃₄ = -338.76 + 1113.289 = 774.529 kJ/kg
(b) The thermal efficiency,
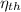 = 1 - T₁/T₂ = (1 - 300/772.467) × 100 ≈ 61.2%
= 1 - T₁/T₂ = (1 - 300/772.467) × 100 ≈ 61.2%
(c) The Mean Effective Pressure, MEP = (Net work)/Displacement Volume)
For unity clearance, volume, we have;
MEP = 774.529/(9 - 1) = 96.816 kPa
(d) The maximum temperature, occur at T₃ = 2655.3 K.