Question

Johnny and Cage are working together to mold figurines for a craft fair. They already have 8 figurines which were left from the last craft fair. Johnny and Cage can mold 3 figurines every hour. Explain the reasons why this situation is linear.

Answer 1

The situation can be described using the equation y = 3x + 8

The rate of change is not constant.

Explanation:

Answer 2

See Explanation

Explanation:

Given

`Initial = 8`

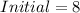
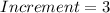`Increment = 3` (every hour)

Required

Explain why it is linear

First, we need to determine the equation that represents the scenario

Let x be the number of hours worked and y be the number of figurines at x hours.

The equation is determined as follows:

`y = Initial\ Figurines + Increment * x`

This gives:

`y = 8 + 3 * x`

`y = 8 + 3x`

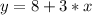
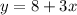
Reorder

`y = 3x + 8`

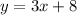
A linear equation is of the form

`y = mx + b`

By comparison,

`y = mx + b` is equivalent to
`y = 3x + 8`

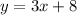
Hence, we can conclude that the situation is linear