Answer:
The zero of the line is (2,0)
Explanation:
The equation of a line passing through points (x1,y1) and (x2,y2) can be found as:
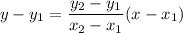
We are given the points (1,-3) and (4,6). Substituting:
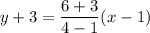
Operating:
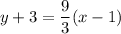
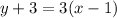
The zero of this line can be found by making y=0 and solving for x:
0+3=3(x-1)
3=3x-3
Adding 3:
6=3x
Solving:
x = 2
The zero of the line is (2,0)