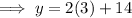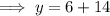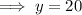Answer:
C. y = 20
Explanation:
Given system of equations:

Multiply the second equation by 3:
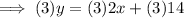
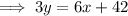
Subtract this from the first equation to eliminate 3y:

Solve the resulting equation for x:
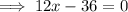
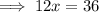

Substitute the found value of x into the original second equation and solve for y: