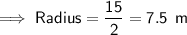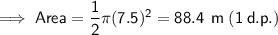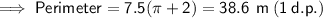Answer:
Formulas
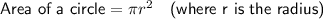
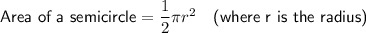
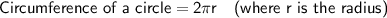
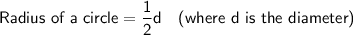
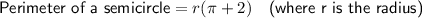
Use the above formulas to calculate the various measurements, remembering to calculate the radius first when given the diameter.
Question 9
a) Radius = 2.7 cm
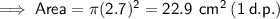
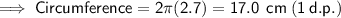
-----------------------------------------------------------------------
b) Diameter = 45 mm
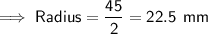
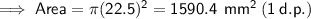
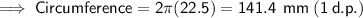
Question 10
a) Radius = 8.5 cm
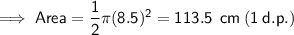
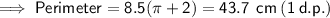
-----------------------------------------------------------------------
b) Radius = 24 mm
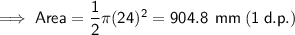
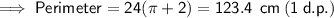
-----------------------------------------------------------------------
c) Diameter = 32 cm
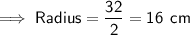
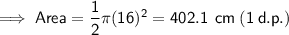
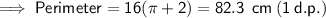
-----------------------------------------------------------------------
d) Diameter = 15 m