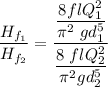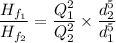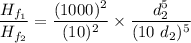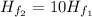Question

Instead of running blood through a single straight vessel for a distance of 2 mm, one mammalian species uses an array of 100 smaller parallel pipes of the same total cross-sectional area, 4.0 mm2. Total volume flow is 1000 mm3/is. The pressure drop for fluid passing through the single pipe is lower than that through the 100 vessel array by a factor of:_____.A. 10.B. 100.

C. 1000.

Answer 1

A. 10

Step-by-step explanation:

For a single straight vessel; we can express the equation as;

`H_(f_1) = (8 \ fl \ Q_1^2)/(\pi ^2 gd_1^5) \ \ \ \ \ ... (1)`

Given that:

The total volume Q₁ = 1000 m/s²

Then the Q₂ = 1000/100 = 10 mm/s₂

However, the question proceeds by stating that 100 pipes of the same cross-section is being used.

Therefore, the formula for the area can be written as:

`(\pi)/(4)d_1^2 = 100 \bigg ( (\pi)/(4) d_2^2\bigg)`

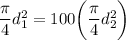
Divide both sides by
`(\pi)/(4)`

`d_1^2 = 100 \ d_2^2`

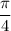
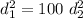
Making
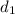`d_1` the subject of the formula;

`d_1 = 10d_2`

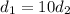
However, considering a pipe in parallel

`H_(f_2) = (H_f_2)_1 = (H_f_2)_2=...= (H_f_2)_(10)= (8 \ fl Q_2^2)/(\pi^2 \ gd _2^5) \ \ \ \ \ \ \ ...(2)`

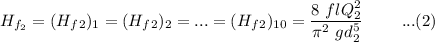
Relating equation (1) by (2); then solving; we have;

`(H_(f_1))/(H_(f_2)) = ((8flQ_1^2)/(\pi^2 \ gd _1^5) )/((8\ fl Q_2^2 )/(\pi^2 gd_2^5) )`

`(H_(f_1))/(H_(f_2)) =(Q_1^2)/(Q_2^2) * (d_2^5)/(d_1^5)`

`(H_(f_1))/(H_(f_2)) =((1000)^2)/((10)^2) * (d_2^5)/((10 \ d_2)^5)`

`(H_(f_1))/(H_(f_2)) =(1)/(10)`

`H_(f_2) =10H_(f_1)`