Answer:
Step-by-step explanation:
From the information given in the question:
The pressure = 1 atm
The saturated humid air temperature
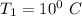
The saturated humid air relative humidity
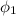 = 100%
= 100%
The atmospheric air temperature
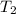 = 32°C; &
= 32°C; &
The atmospheric relative humidity
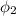 = 80%
= 80%
The data obtained at 1 atm pressure from property psychometric chart at
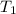 = 10°C
= 10°C
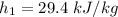 of air ;
of air ;
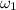 = 0.0077 kg/kg of air
= 0.0077 kg/kg of air
At
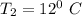
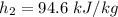 of air;
of air;
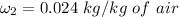
If we take a look at the expression used in combining the conservation of energy and mass for adiabatic mixing of two streams; we have:
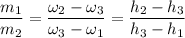
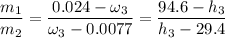
The mixture temperature
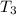 is determined through a trial and error method.
is determined through a trial and error method.
At trial and error method
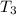 = 24°C
= 24°C
From the relative humidity of 70%;
From the psychometric chart;
The specific humidity
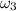 = 0.0143 kg/kg of air
= 0.0143 kg/kg of air
The enthalpy
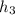 = 57.6 kJ/kg of air
= 57.6 kJ/kg of air
Then;
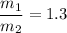
Thus, 1.3 is the proportion at which the two streams are being mixed.