Question

Using the inverse of sine, cosine and tangent allow us to find A missing side in a right triangle A missing angle in a right triangle The perimeter of a right triangle Triangular area

Answer 1

A missing angle in a right angle.

Explanation:

Given, the inverse of trigonometric functions sine, cosine and tangent.

To find:

The value that can be found using the inverse trigonometric functions.

Solution:

First of all, let us consider the right angled triangle attached in answer area.

Hypotenuse is AC, Base is BC and AB is the Altitude/Height of the right angled
`\triangle ABC`.

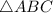Let us suppose all three sides are known and
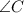`\angle C` is unknown.

Formula:

`1.\ sin\theta = (Perpendicular)/(Hypotenuse)`

`2.\ cos\theta = (Base)/(Hypotenuse)`

`3.\ tan\theta = (Perpendicular)/(Base)`

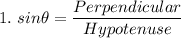
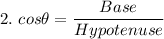
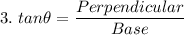
Let us consider
`\angle C`.

`sin C = (AB)/(BC)`

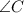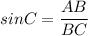
If we taken inverse:

`sin^(-1) sinC = sin^(-1) ((AB)/(BC))`

`\Rightarrow \angle C = sin^1(AB)/(BC)`

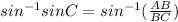
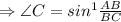
Similar is the case for cosine and tangent.

Therefore, the missing angle of the right angled triangle can be calculated by the inverse of sine, cosine and tangent.