Answer:
Approximately
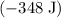 , assuming that the bike was on level ground.
, assuming that the bike was on level ground.
Step-by-step explanation:
If an object of mass
 is moving at a speed of
is moving at a speed of
 , the kinetic energy of that object would be
, the kinetic energy of that object would be
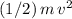 .
.
At a speed of
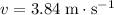 , the kinetic energy of the bike and the cyclist- combined- would be:
, the kinetic energy of the bike and the cyclist- combined- would be:
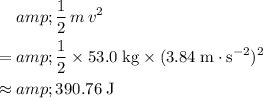 .
.
At a speed of
 , the kinetic energy of the bike and the cyclist- combined- would be:
, the kinetic energy of the bike and the cyclist- combined- would be:
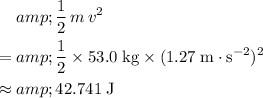 .
.
The energy change was approximately:
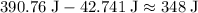 .
.
If the bike was on level ground, the friction on the bike and the cyclist would have done a work of
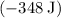 to reduce the kinetic energy of the bike and the cyclist by that amount.
to reduce the kinetic energy of the bike and the cyclist by that amount.