The equation in point-slope form for the line perpendicular to
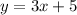 that passes through
that passes through
 is
is
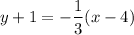 .
.
Determine the slope of the original line: The coefficient of x in the equation
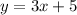 is 3.
is 3.
Find the slope of the line perpendicular to the original line: The slope of a line perpendicular to another line is the negative reciprocal of its slope. So, the slope of the line perpendicular to y=3x+5 is
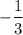 .
.
Use the point-slope form of a linear equation: The point-slope form is given by
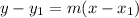 , where
, where
 is a point on the line and m is the slope.
is a point on the line and m is the slope.
Substitute the values into the point-slope form: Substituting $(4,-1)$ as the point and
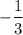 as the slope, we get
as the slope, we get
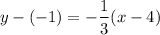 .
.
Simplify the equation: Simplifying the equation gives
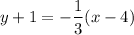 .
.
Therefore, the equation in point-slope form for the line perpendicular to y=3x+5 that passes through (4,-1) is:
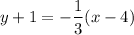 .
.
So, the correct answer is option C.