Question

Write the solution set in interval notation.

Answer 1

First, you need to solve the inequalities.

`4q\geq -16`

`q\geq -4`

`q+3<7`

`q<4`

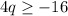
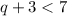
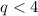
Now let's write the interval notation for the first one.

The lowest number for this would be -4. q cannot be less than negative -4. Since q can be -4 OR greater than, you use brackets. [-4,

q can be anything greater than -4. So the second number is infinity. Infinity uses parentheses because it is no exact number.

So the interval notation for the first inequality is [-4, ∞).

Now let's write the interval notation for the second one.

q can be anything less than 4. So the first number would be negative infinity: (-∞

q cannot pass 4, so the second number would be 4. Since q does not include 4, you use parentheses: 4)

The interval notation for the second inequality is (-∞, 4).

The interval notation for this compound inequality is [-4, ∞) or (-∞, 4).

Sorry if this was long and confusing. Hope this helped!