Answer:
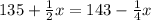
Explanation:
Let E represent Erin’s weight, and let M reprevent Miranda’s weight.
And let x represent the amount of week that passes.
Eric is currently 135 pounds. However, she is gaining 1/2 pounds per week x.
Hence, we can write the following equation:
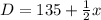
Miranda currently weights 143 pounts. However, she is losing 1/4 pounds per week x.
Since she is losing weight, 1/4 is negative. Hence:
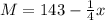
When the two girls weigh the same, D=M. Thus:
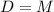
Substitute them for their respective equations to acquire:
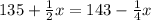
Notes:
To solve, first eliminate the fractions by multiplying everything by 4. This yields:
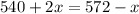
Add x to both sides. Subtract 540 from both sides:

Divide both sides by 3:

Hence, it will take about 11 weeks for the girls to weigh the same.