Question

Which function is the result of translating f(x) = x^2 + 14 to the right 5 units and down 6 units?

A) y = (x - 5)^2 + 6
B) y = (x - 5)^2 - 6
C) y= (x - 5)^2 + 8
D) y= (x - 5)^2 + 20

Answer 1

C) y= (x - 5)^2 + 8

Explanation:

Answer 2

C.

Explanation:

Transformations within the quadratic is given by the form:

`y=a(x-h)^2+k`

Where a is the vertical stretch, h is the horizontal translations, and k is the vertical translations.

We have:

`y=x^2+14`

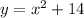
If we translate this 5 units to the right, we are letting h=5. This yields:

`y=(x-5)^2+14`

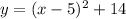
If we shift the function down 6 units, we are subtracting 6 from the function. This will yield:

`y=(x-5)^2+14-6`

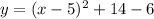
Subtract:

`y=(x-5)^2+8`

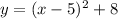
Therefore, our answer is C.