Question

A square poster has an area measure of 324x^2 + 540x + 225 square units. Determine the side length of the poster.

Answer 1

`\huge\text{$(18x+15)$ units}`

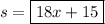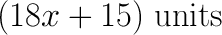
Given the area, we need to find the side length. Let's start with the area equation for a square, where
`s` is the side length and
`A` is the area.

`s^2=A`

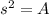
Substitute in the known value.

`s^2=324x^2+540x+225`

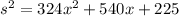
Now we need to factor the trinomial. The trinomial given for the area is a perfect square trinomial since
`324` (
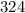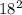`18^2`) and
`225` (
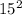`15^2`) are both perfect squares.

We also know that
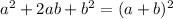`a^2+2ab+b^2=(a+b)^2`, which we can use to factor.

`s^2=324x^2+540x+225\\s^2=(18x)^2+2(18x)(15)+15^2\\s^2=(18x+15)^2`

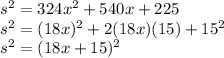
Now, take the square root of both sides to fully isolate
`s`.

`√(s^2)=√((18x+15)^2)`

Keep in mind that the square root of any value squared is the original value.

`s=\boxed{18x+15}`