Question

((sinx+cosx)^2)/sinxcosx=2+secxcosecx​

Answer 1

Proof below

Explanation:

Trigonometric Identities

Prove that:

`\displaystyle ((\sin x+\cos x)^2)/(\sin x\cos x)=2+\sec x\csc x`

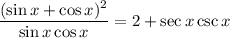
We need to use the following basic identities:

`\sin^2x+\cos^2x=1\qquad\qquad [1]`

`\displaystyle \sec x=(1)/(\cos x)\qquad\qquad [2]`

`\displaystyle \csc x=(1)/(\sin x)\qquad\qquad [3]`

Operating on the left side:

`\displaystyle ((\sin x+\cos x)^2)/(\sin x\cos x)=(\sin^2 x+2\cos x\sin x+\cos^2x)/(\sin x\cos x)`

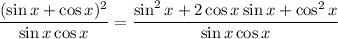
Applying [1]:

`\displaystyle ((\sin x+\cos x)^2)/(\sin x\cos x)=(1+2\cos x\sin x)/(\sin x\cos x)`

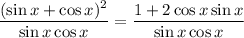
Separating fractions:

`\displaystyle ((\sin x+\cos x)^2)/(\sin x\cos x)=(1)/(\sin x\cos x)+(2\cos x\sin x)/(\sin x\cos x)`

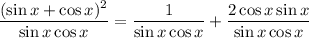
Simplifying the second term:

`\displaystyle ((\sin x+\cos x)^2)/(\sin x\cos x)=(1)/(\sin x\cos x)+2`

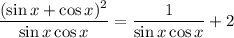
Applying [2] and [3]

`\displaystyle ((\sin x+\cos x)^2)/(\sin x\cos x)=\csc x\sec x+2`

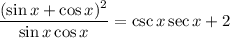
Rearranging:

`\displaystyle ((\sin x+\cos x)^2)/(\sin x\cos x)=2+\sec x\csc x`

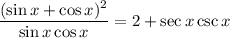
Hence proved.