Question

Two points on a line are (-7,10)and (9,2). Two points on a line parallel to that line are are (1,3) and (x,4). What is the value of x

Answer 1

x = -1

Explanation:

When two lines are parallel, they have the same slope. To find the value of x, we first have to find the slope of the other line. We can do this by inputting the given points (-7, 10) and (9, 2) into the expression
`(y2-y1)/(x2-x1)`:

`(10-2)/(-7-9)`

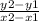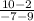
Solve:

10 - 2 = 8

-7 - 9 = -16

8/-16 can be simplified to -1/2.

The slope of the first line is -1/2. Now we can input the points (1, 3) (x, 4) into the expression used to find slope and equal that expression to the value of the first line's slope. We can do this because we know the slopes will be equal to each other.

`(4-3)/(x-1)` = -
`(1)/(2)`

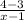First simplify the left side:

4 - 3 = 1

`(1)/(x-1)` = -
`(1)/(2)`

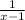Now, multiply both sides of the equation by x - 1 to isolate the x on the right side of the equation:

1 =
`(-x+1)/(2)`

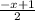
Multiply both sides by 2:

2 = -x + 1

Subtract 1 from both sides:

1 = -x

Divide both sides by -1 to isolate the x:

-1 = x

The value of x is -1.

To check if our answer is correct we can put the value of x back into the expression used to find slope:

`(4-3)/(x-1)`

`(4-3)/(-1-1)`

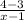
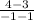
Solve:

4 - 3 = 1

-1 - 1 = -2

The slope of the second line is -1/2, which is the same as the slope of the first line, which means that our answer is correct.

Hope this helps :)