Question

When Noah goes bowling, his scores are normally distributed with a mean of 150 and a standard deviation of 12. What is the probability that the next game Noah bowls, his score will be between 135 and 167, to the nearest thousandth?

Answer 1

The probability of his score being between 135 and 167 is 0.8151 or (0.8151*100=81.51%)

Explanation:

Given that:

Mean = μ = 150

SD = σ = 12

Let x1 be the first data point and x2 the second data point

We have to find the z-scores for both data points

x1 = 135

x2 = 167

So,

`z_1 = (x_1-mean)/(SD)\\= (135-150)/(12)\\=(-15)/(12)\\=-1.25`

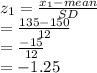
And

`z_2 = (x_2-mean)/(SD)\\z_2 =(167-150)/(12)\\=(17)/(12)\\= {1.416}`

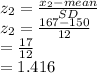
We have to find area to the left of both points then their difference to find the probability.

So,

Area to the left of z1 = 0.1056

Area to the left of z2 = 0.9207

Probability to score between 135 and 167 = z2-z1 = 0.9027-0.1056 = 0.8151

Hence,

The probability of his score being between 135 and 167 is 0.8151 or (0.8151*100=81.51%)