Answer:

Keys:
For this problem, you need the quadratic formula(listed below).
When you see ± in a quadratic equation, you must know there is going to be at least 2 solutions.
Explanation:
solving for x₁ and x₂

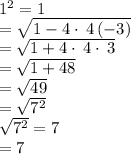
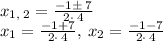
solve for x₁

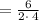
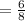
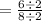

solve for x₂
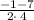

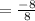
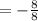

Hope this helps!