Question

The sum of three consecutive odd numbers is 63. Find the numbers.

I need full explanation:)​

Answer 1

19, 21, 23

Explanation:

Let the first odd number be n.

Then the second, consecutive odd number will be (n+2).

And the third will be (n+4).

We know that they sum to 63. Hence, we can write the following equation:

`n+(n+2)+(n+4)=63`

Solve for n. Combine like terms:

`3n+6=63`

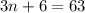
Subtract 6 from both sides:

`3n=57`

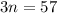
Divide both sides by 3:

`n=19`

Hence, the first odd number is 19.

Therefore, our sequence is: 19, 21, 23.

Note: If we get an even or non-integer value for our n, then there are no three consecutive odd integers that exists that sum to 63.

Answer 2

Required Answer:

19,21,23

Question:

The sum of three consecutive odd numbers is 63. Find the numbers.

Given:

• sum of three consecutive odd numbers = 63

Let:

Three consecutive odd numbers be:

• x
• x+2
• x+4

A/Q

sum of three consecutive odd numbers is 63

.°. x+(x+2)+(x+4)=63

→x+x+x=63-2-4

→3x=63-6

→3x=57

→x=57/3

→x=19

We get value of x → 19

Now put values in each number

First odd number= x

.°.First odd number=19

Second odd number =x+2

.°. Second odd number= 19+2

Second odd number = 21

Third odd number =x+4

.°.Third odd number=19+4

Third odd number=23

hope it helps!♡