Question

A ball is thrown directly downward at 4 m/s from the edge of a high cliff. If needed, use g = 10 m/s2. With zero air resistance, the distance the ball falls during its third second of fall is most nearly

28 m
4 m
29 m
12 m
57 m

Answer 1

57 meters

Step-by-step explanation:

Let's see what variables we have in this problem:

• 
  `v_i \ \ \ \ \ \ \ t \\ v_f \ \ \ \ \ \ \triangle x \\ a`

Let's set the upwards direction to be positive and the downwards direction to be negative.

We are given the initial velocity, 4 m/s. Since the ball is thrown directly downward, we can say that the initial velocity = -4 m/s.

We are also given the acceleration due to gravity, and since the acceleration is pointing downwards, we can say that a = -10 m/s².

The time is also given to us; the question wants to know the vertical displacement at time = 3 seconds, so we can plug in 3 seconds for t.

Since we are solving for vertical displacement, we can use
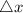`\triangle x` as one of our variables.

Now we have all of the variables except for the final velocity,
`v_f`.

Since we are dealing with constant acceleration, we can use this constant acceleration equation:

• 
  `x_f=x_i+v_it+(1)/(2)at^2`

Subtract
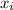`x_i` from both sides to get
`\triangle x`.

• 
  `\triangle x =v_it+(1)/(2)at^2`

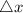Substitute in the known values:

• 
  `\triangle x = (-4(m)/(s))(3s) + (1)/(2)(-10(m)/(s^2))(3s)^2`

Get rid of the units to make the equation more readable.

• 
  `\triangle x = (-4)(3) + (1)/(2) (-10)(3)^2`

Simplify the equation and solve for delta x.

• 
  `\triangle x=(-12) -5(9)`
• 
  `\triangle x =-12-45`
• 
  `\triangle x = -57`

The vertical displacement is -57 meters, so we can say that the distance the ball falls in 3 seconds is most nearly 57 meters.