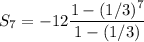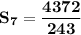Question

Pleasee help mee ;-; i can't stand algebra, determine how many terms the geometric series has, and then find the sum of the series

-12 -4 - 4/3 - . . . - 4/243

Answer 1

The series has 7 terms

`\displaystyle S_7=(4372)/(243)`

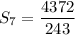
Explanation:

Geometric Series

In the geometric series, each term is found by multiplying (or dividing) the previous term by a fixed number, called the common ratio.

We are given the series:

-12, -4, -4/3, ..., -4/243

We can find the common ratio by dividing one term by the previous term:

`\displaystyle r=(-4)/(-12)`

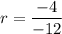
Simplifying:

`\displaystyle r=(1)/(3)`

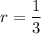
Sum of terms: Given a geometric series with first term a1 and common ratio r, the sum of n terms is:

`\displaystyle S_n=a_1(1-r^n)/(1-r)`

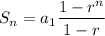
We need to find how many terms the series has. Using the explicit formula of a geometric series:

`a_n=a_1\cdot r^(n-1)`

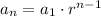
The last term is an=-4/243 and the first term is a1=-12. Solving for n:

`\displaystyle n= (\log(a_n/a_1))/(\log r)+1`

`\displaystyle (\log(-4/243/-12))/(\log 1/3)+1`

`\displaystyle (\log(1/729))/(\log 1/3)+1`

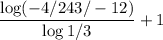
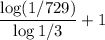
n=7

The series has 7 terms

Thus, the sum of the 7 terms of the series is:

`\displaystyle S_7=-12(1-(1/3)^7)/(1-(1/3))`

`\mathbf{\displaystyle S_7=(4372)/(243)}`