Answer:
sin ∠FDE is 12/13
Explanation:
The trigonometric ratios will be used to find the value of sin∠FDE
In the given triangle, according to angle FDE
Base = DE = 5
Hypotenuse = DF = 13
Perpendicular = EF = ?
sin ∠FDE =
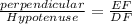
We have to find the length of DF first
Pythagoras theorem will be used as the given triangle is a right angled triangle
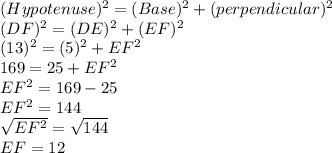
So,
sin ∠FDE = EF/DF
sin ∠FDE = 12/13
Hence,
sin ∠FDE is 12/13