Question

A right triangle, DEF, is shown below.
What is sin FDE?

Answer 1

sin ∠FDE is 12/13

Explanation:

The trigonometric ratios will be used to find the value of sin∠FDE

In the given triangle, according to angle FDE

Base = DE = 5

Hypotenuse = DF = 13

Perpendicular = EF = ?

sin ∠FDE =
`(perpendicular)/(Hypotenuse) = (EF)/(DF)`

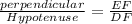
We have to find the length of DF first

Pythagoras theorem will be used as the given triangle is a right angled triangle

`(Hypotenuse)^2 = (Base)^2+(perpendicular)^2\\(DF)^2 = (DE)^2+(EF)^2\\(13)^2 = (5)^2 + EF^2\\169 = 25+EF^2\\EF^2 = 169-25\\EF^2 = 144\\√(EF^2) = √(144)\\EF = 12`

So,

sin ∠FDE = EF/DF

sin ∠FDE = 12/13

Hence,

sin ∠FDE is 12/13