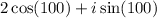Answer:
The answer is
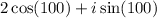
Explanation:
This is a complex number,
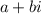
First, convert this to de movire form.
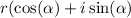
where
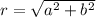
and
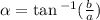

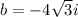

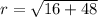
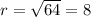
and
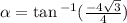
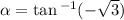
Here, our a is positive and b is negative so our angle in degrees must lie in the fourth quadrant, that angle is 300 degrees.
So
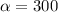
So our initially form is

Now, we use the roots of unity formula. To do this, we first take the cube root of the modulus, 8,
![\sqrt[3]{8} = 2](https://img.qammunity.org/2023/formulas/mathematics/high-school/b10jabmbct3m14pzdd29nvn384s9hhowip.png)
Next, since cos and sin have a period of 360 we add 360 to each degree then we divide it by 3.
![\sqrt[3]{8} ( \cos( (300 + 360n)/(3) ) + \sin( (300 + 360n)/(3) )](https://img.qammunity.org/2023/formulas/mathematics/high-school/hxqsypcs28eipznr3j8s8h481qcozdlgbl.png)
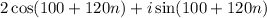
Since 100 is in the second quadrant, we let n=0,