Question

HELP ASAP?!?!?!? QUADRATIC REGRESSION MODELS

Make a scatter plot of the data below

(10,12.5)
(20,36)
(30,69.5)
(40,114)
(50,169.5)
(60,249)
(70,325.5)

Use the quadratic regression feature of a graphing calculator to find a quadratic model. Round to the nearest hundredths place.​

Answer 1

4.87138

Step-by-step explanation:

i think

Answer 2

1. After creating a scatter plot of the provided data points and using the quadratic regression feature on a graphing calculator, the quadratic model obtained is approximately
`\( y = 1.01x^2 + 3.45x - 1.18 \)`.

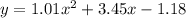Step-by-step explanation:

Quadratic regression models are used to fit a quadratic function to a set of data points. The provided data points are 10,12.5, 20,36, 30,69.5, 40,114, 50,169.5, 60,249, 70,325.5. To create a scatter plot, each point is plotted on the coordinate plane. The quadratic regression feature of a graphing calculator is then used to find the quadratic model that best fits the data.

3.Calculation and Interpretation:

Using a graphing calculator, the quadratic model obtained is
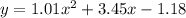`y = 1.01x^2 + 3.45x - 1.18 \)`rounded to the nearest hundredths. This model represents the best-fitting quadratic curve for the given data. The coefficients in the quadratic equation provide information about the shape, direction, and position of the parabolic curve.

Therefore, the quadratic model derived from the regression analysis is
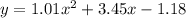`\( y = 1.01x^2 + 3.45x - 1.18 \)`, and this equation can be used to make predictions or analyze the relationship between the variables represented by the data points.