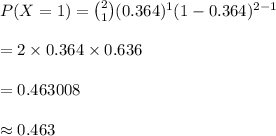Question

A box of 11 transistors has 4 defective ones.

A) If 2 transistors are drawn from the box together, what is the probability that both transistors are defective?
B) If 2 transistors are drawn from the box together, what is the probability that neither transistor is defective?
C) If 2 transistors are drawn from the box together, what is the probability that one transistor is defective?

Answer 1

(a) 0.1325

(b) 0.4045

(c) 0.463

Explanation:

Let X denote the number of defective transistors.

The proportion of defective transistors is, p = 4/11 = 0.364.

All the transistors are independent of the others.

The random variable X follows a binomial distribution.

(a)

Compute the probability that both transistors are defective, if 2 transistors are drawn from the box together as follows:

`P(X=2)={2\choose 2}(0.364)^(2)(1-0.364)^(2-2)\\\\=1* 0.132496* 1\\\\=0.132496\\\\\approx 0.1325`

(b)

Compute the probability that neither transistors are defective, if 2 transistors are drawn from the box together as follows:

`P(X=0)={2\choose 0}(0.364)^(0)(1-0.364)^(2-0)\\\\=1* 1* 0.404496\\\\=0.404496\\\\\approx 0.4045`

(c)

Compute the probability that one transistors are defective, if 2 transistors are drawn from the box together as follows:

`P(X=1)={2\choose 1}(0.364)^(1)(1-0.364)^(2-1)\\\\=2* 0.364* 0.636\\\\=0.463008\\\\\approx 0.463`