Step-by-step explanation:
Hey there!
Given;
Mass of the Earth (M) = 6.0*10^24kg.
Radius of Earth (R) = 6400km = 6400*1000= 6.4*10^6.
Gravitational constant (G) = 6.67*10^-11Nm^2/kg^2.
Height from surface of Earth (h) = 350km= 3.5*10^5m
Gravity (g) = ?
We have;
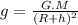
Where "G" is gravitational constant, "M" is mass of earth, "g" is acceleration due to gravity, "h" height from surface of Earth.
Keep all values.
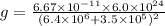
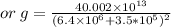
g = 8.7m/s^2
Therefore, gravity from distance 350km above the Earth's surface is 8.7m/s^2.
Hope it helps...