Question

I just need help with question one, but if you want to you can answer question 2 as well. I’ll give 100 points!

Answer 1

Translations

For
`a > 0`

`f(x+a) \implies f(x) \: \textsf{translated}\:a\:\textsf{units left}`

`f(x-a) \implies f(x) \: \textsf{translated}\:a\:\textsf{units right}`

`f(x)+a \implies f(x) \: \textsf{translated}\:a\:\textsf{units up}`

`f(x)-a \implies f(x) \: \textsf{translated}\:a\:\textsf{units down}`

`y=a\:f(x) \implies f(x) \: \textsf{stretched parallel to the y-axis (vertically) by a factor of}\:a`

`y=f(ax) \implies f(x) \: \textsf{stretched parallel to the x-axis (horizontally) by a factor of} \: (1)/(a)`

`y=-f(x) \implies f(x) \: \textsf{reflected in the} \: x \textsf{-axis}`

`y=f(-x) \implies f(x) \: \textsf{reflected in the} \: y \textsf{-axis}`

Question 1

Given:
`f(x)=(2,-3)`

`f(x)+2 \implies (x, y+2)= (2,-3+2)=(2,-1)`

`f(x)-3 \implies (x,y-3)=(2,-3-3)=(2,-6)`

`f(x+5)\implies (x-5,y)=(2-5,-3)=(-3,-3)`

`-f(x) \implies (x,-y)=(2,-(-3))=(2,3)`

`f(-x) \implies (-x,y)=(-(2),-3)=(-2,-3)`

`f(2x) \implies \left((x)/(2),y\right)=\left((2)/(2),-3\right)=(1,-3)`

`2f(x) \implies (x,2y)=(2,2 \cdot -3)=(2,-6)`

`-f(x-4) \implies (x+4,-y)=(2+4,-(-3))=(6,3)`

Question 2

Parent function:
`y=x^2`

Given function:
`f(x)=(x+8)^2-4`

`f(x+8) \implies f(x) \: \textsf{translated}\:8\:\textsf{units left}`

`f(x)-4 \implies f(x) \: \textsf{translated}\:4\:\textsf{units down}`

Therefore, a translation 8 units to the left and 4 units down.

Answer 2

Step-by-step explanation:

Given f(x) : (2, -3)

Translation's:

f(x) + 2 then graph translates up by 2 units up =
`\boxed{\sf (2, -1)}`

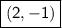
f(x) - 3 then graph translates down 3 units down =
`\boxed{\sf (2, -6)}`

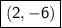
f(x + 5) then graph translates left 5 units =
`\boxed{\sf (-3, -3)}`

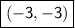
-f(x) then graph reflects over x axis =
`\sf \boxed{\sf (2, 3)}`

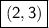
f(-x) then graph reflects over y axis =
`\sf \boxed{\sf (-2,-3)}`

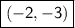
f(2x) then graph has horizontal compression = (2/2, -3) =
`\boxed{\sf (1, -3)}`

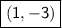
2f(x) then graph has vertical compression = (2, (-3)2) =
`\boxed{\sf (2, -6)}`

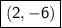
-f(x - 4) then graph reflects over x axis, moves 4 units to right =
`\sf \boxed{\sf (6, 3)}`

Solution 2

Parent function: y = x²

Graph function: f(x) = (x + 8)² - 4

After Identification:

D. The graph has a translation of 8 units left and 4 units down.