Question

Solve the system by elimination. need work to be shown

Answer 1

x=1, y=1, z=0

Explanation:

System of Equations

We are required to solve the system of equations by elimination:

`\left\{\begin{matrix}-2x+2y+3z=0\qquad [1]\\-2x-y+z=-3 \qquad [2]\\2x+3y+3z=5 \qquad [3]\end{matrix}\right`

Adding [1] and [3], and subtracting [1] and [2]:

`\left\{\begin{matrix}5y+6z=5\qquad [4]\\3y+2z=3\qquad [5] \end{matrix}\right.`

Multiplying [5] by -3 and adding to [4]:

`-4y=-4`

Solving:

`y = -4 / (-4) = 1`

`y=1`

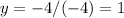
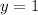
Substituting into [5]:

`5(1)+6z=5`

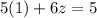
Simplifying:

`6z = 0`

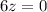
z=0

Substituting into [3]

`2x+3(1)+3(0)=5`

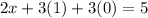
Operating:

`2x+3=5`

`2x = 2`

`x = 2/2=1`

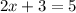
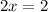
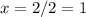
x=1

The solution is

x=1, y=1, z=0