Answer:
x=1, y=1, z=0
Explanation:
System of Equations
We are required to solve the system of equations by elimination:
![\left\{\begin{matrix}-2x+2y+3z=0\qquad [1]\\-2x-y+z=-3 \qquad [2]\\2x+3y+3z=5 \qquad [3]\end{matrix}\right](https://img.qammunity.org/2021/formulas/mathematics/college/vfhkoqzxgl4xa1wnxyo5lvu85qkjldqblu.png)
Adding [1] and [3], and subtracting [1] and [2]:
![\left\{\begin{matrix}5y+6z=5\qquad [4]\\3y+2z=3\qquad [5] \end{matrix}\right.](https://img.qammunity.org/2021/formulas/mathematics/college/9p74w7yt9xfeekiihcto5pqrf5h703ykl0.png)
Multiplying [5] by -3 and adding to [4]:
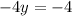
Solving:
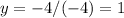
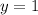
Substituting into [5]:
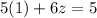
Simplifying:
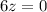
z=0
Substituting into [3]
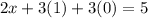
Operating:
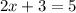
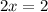
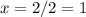
x=1
The solution is
x=1, y=1, z=0