Answer:
D The volume of a cube increases by a factor of 8 when its edge length doubles
Explanation:
Volume of a cube is represented by the function
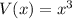
where
 represents the edge length of the cube
represents the edge length of the cube
Now when
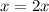 i.e., when the edge length is doubled we have
i.e., when the edge length is doubled we have
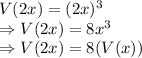
It can be seen that the volume of the cube increased by 8 times when edge length doubles.