Question

The volume of a cube can be written as a function of its edge length, V(x) = x^3. Which is a correct interpretation of V(2x)?

(A) The volume of a cube doubles when its edge length doubles.
B) The volume of a cube increases by a factor of 4 when its edge length doubles.
©
The volume of a cube increases by a factor of 6 when its edge length doubles.
D The volume of a cube increases by a factor of 8 when its edge length doubles.

Answer 1

the answer is d

Explanation:

Answer 2

D The volume of a cube increases by a factor of 8 when its edge length doubles

Explanation:

Volume of a cube is represented by the function

`V(x)=x^3`

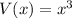
where
`x` represents the edge length of the cube

Now when
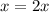`x=2x` i.e., when the edge length is doubled we have

`V(2x)=(2x)^3\\\Rightarrow V(2x)=8x^3\\\Rightarrow V(2x)=8(V(x))`

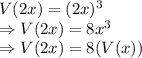
It can be seen that the volume of the cube increased by 8 times when edge length doubles.