Question

A cylindrical tank, 0.42 m in diameter, drains through a hole in its bottom. At the instant when the water depth is 0.73 m, the flow rate from the tank is observed to be 5 kg/s. Determine the rate of change of water level at this instant.

Answer 1

The rate of change of water level at this instant is approximately -0.036 meters per second.

Step-by-step explanation:

From this problem we know that outflow mass rate of water, current depth of water within the tank and the diameter of the cylindrical tank. From Physics we get the equation for the current mass of water inside the tank:

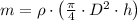`m = \rho \cdot \left((\pi)/(4)\cdot D^(2)\cdot h \right)` (1)

Where:

`m` - Current mass of water inside the tank, measured in kilograms.

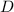`D` - Diameter of the cylindrical tank, measured in meters.

`h` - Depth of the water in the tank, measured in meters.

By differentiation in time, we derive the expression for the mass outflow of water (
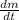`(dm)/(dt)`), measured in kilograms per second, by considering geometric characteristics of the cylinder (
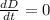`(dD)/(dt) = 0`) and the fact that water is an incompressible fluid (
`(d\rho)/(dt) = 0`):

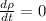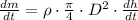`(dm)/(dt) = \rho \cdot (\pi)/(4) \cdot D^(2)\cdot (dh)/(dt)` (2)

Where
`(dh)/(dt)` is the rate of change of water level, measured in meters per second.

If we know that
`\rho = 1000\,(kg)/(m^(3))`,
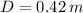`D = 0.42\,m` and
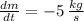`(dm)/(dt) = - 5\,(kg)/(s)`, then the rate of change of water level is:

`(dh)/(dt) = (4)/(\pi \cdot \rho\cdot D^(2)) \cdot (dm)/(dt)`

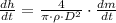
`(dh)/(dt) = \left[(4)/(\pi\cdot \left(1000\,(kg)/(m^(3)) \right)\cdot (0.42\,m)^(2)) \right]\cdot (-5\,(kg)/(s) )`

`(dh)/(dt) \approx -0.036\,(m)/(s)`

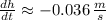
The rate of change of water level at this instant is approximately -0.036 meters per second.