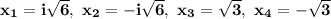Question

ANSWER ASAP PLEASE & SHOW UR WORK!!!

Find the real or imaginary solutions. x^4 + 3x^2 - 18 = 0

Answer 1

`x_1=\mathbf{i}√(6),\ x_2=-\mathbf{i}√(6),\ x_3=√(3),\ x_4=-√(3)`

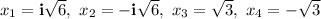
Explanation:

Biquadratic Equations

Solve:

`x^4 + 3x^2 - 18 = 0`

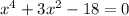
The biquadratic equations are equations of degree 4 without the terms of degree 1 and 3.

Solving such equations requires to express the equation as a second-degree equation with
`x^2` as the variable.

Rewriting the equation:

`(x^2)^2 + 3(x^2) - 18 = 0`

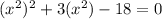
The quadratic equation can be factored as:

`(x^2+6)(x^2-3)=0`

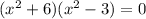
It leads to two equations:

`x^2+6=0`

`x^2-3=0`

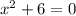
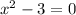
The first equation has imaginary roots. Solving for x:

`x^2=-6`

`x=\pm√(-6)`

`x_1=\mathbf{i}√(6)`

`x_2=-\mathbf{i}√(6)`

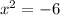
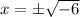
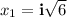
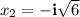
Where

`\mathbf{i}=√(-1)`

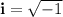
The second equation has two real roots:

`x^2-3=0`

`x^2=3`

`x=\pm√(3)`

`x_3=√(3)`

`x_4=-√(3)`

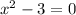
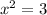
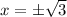
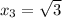
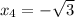
The roots are:

`\mathbf{x_1=\mathbf{i}√(6),\ x_2=-\mathbf{i}√(6),\ x_3=√(3),\ x_4=-√(3)}`