Answer:
f(-x)= -f(x) so, the given function
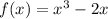 is Odd
is Odd
Explanation:
We need to determine if the function
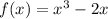 is Even, Odd, or Neither.
is Even, Odd, or Neither.
Determining if a function f(x) is even or not we put x=-x and check
If f(-x)=f(x) the function is even
if f(-x)= -f(x) the function is odd
So, Putting x =-x and determining if the given function
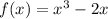 is Even, Odd, or Neither.
is Even, Odd, or Neither.
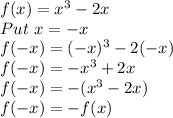
As f(-x)= -f(x) so, the given function
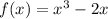 is Odd
is Odd