Question

Find the maximum height of the rocket and explain in at least threes sentence how you calculated your answer of y = - 16x ^ 2 + 480x

Answer 1

The maximum height of the rocket is 3600

Explanation:

The vertex of the quadratic equation y = ax² + bx + c is (h, k), where

• h =
  `(-b)/(2a)`

• k = y at x = h

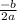
• The vertex (h, k) is a minimum point if a is positive

• The vertex (h, k) is a maximum point if a is negative

The height of the rocket calculated using the equation y = -16x² + 480x, where y is the height and x is the time

To find the maximum height, do that

1. Find the x-coordinate of the vertex of the equation ⇒ h
2. Substitute the value of x in the equation by h to find the y-coordinate of the equation ⇒ k
3. The maximum height equal the value of k

Let us do that

∵ y = -16x² + 480x

∴ a = -16 ⇒ the vertex is a maximum point

∴ b = 480

→ Use the rule above to find h

∵ h =
`(-b)/(2a)`

∴ h =
`(-480)/(2(-16))` =
`(-480)/(-32)`

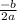
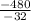
∴ h = 15

∵ k = y at x = h

→ Substitute x by 15 in the equatuion and y by k to find x

∵ k = -16(15)² + 480(15)

∴ k = -3600 + 7200

∴ k = 3600

∵ The maximum height equal the value of k

∴ The maximum height of the rocket is 3600