Answer:
As the height of warehouse is greater than the height of crate, the crate will fit in the warehouse.
Explanation:
Given that
Volume of cube = V = 2197 cubic feet
Side of cube = a =?
Height of ware house = h = 14 feet
In order for the crate to fit in the warehouse the height of crate has to be less than the height of warehouse i.e. a<h
In order to check this we have to find the side/height of crate
So,
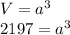
Taking cube root on both sides
![\sqrt[3]{a^3} = \sqrt[3]{2197}\\\sqrt[3]{a^3} = \sqrt[3]{13^3}\\ a = 13\ feet](https://img.qammunity.org/2021/formulas/mathematics/high-school/x1vsb7tdnth9ntclby024qsnj0r8o5aqr1.png)
So the height of cube is 13 feet.
Comparing the height of c and height of ware house we can conclude that
Height of Warehouse > Height of crate
h>a
14>13
As the height of warehouse is greater than the height of crate, the crate will fit in the warehouse.