Question

Please help, this chapter was on derivatives...

Answer 1

(3) Differentiating both sides of

`2x^(3/2) + y^(3/2) = 29`

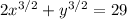
with respect to x gives

`3x^(1/2) + \frac32 y^(1/2) (\mathrm dy)/(\mathrm dx) = 0`

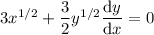
Solve for dy/dx :

`\frac32 y^(1/2) (\mathrm dy)/(\mathrm dx) = -3x^(1/2) \\\\ (\mathrm dy)/(\mathrm dx) = (-3x^(1/2))/(\frac32y^(1/2)) = (-2x^(1/2))/(y^(1/2)) = -2√(\frac xy)`

Then the slope of the tangent line to the curve at (1, 9) is

`(\mathrm dy)/(\mathrm dx) = -2√(\frac19) = -\frac23`

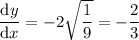
The equation of the tangent line would then be

y - 9 = -2/3 (x - 1) ==> y = -2/3 x + 29/3

(4) The slope of the tangent line to

`y=(ax+1)/(x-2)`

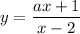
at a point (x, y) on the curve is

`(\mathrm dy)/(\mathrm dx) = (a(x-2)-(ax+1))/((x-2)^2) = -(2a+1)/((x-2)^2)`

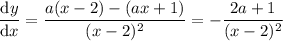
When x = -1, we have a slope of 2/3, so

-(2a + 1)/(-1 - 2)² = 2/3

Solve for a :

-(2a + 1)/9 = 2/3

2a + 1 = -18/3 = -6

2a = -7

a = -7/2