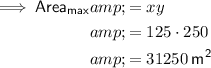Answer:
Dimensions: 125 m x 250 m
Area: 31,250 m²
Explanation:
Given information:
- Total amount of fencing = 500m
- Only 3 sides of the land need to be fenced
First, let us assume that the land is rectangular in shape.
Let
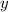 = length of the side opposite the river
= length of the side opposite the river
Let
 = length of the other 2 sides of the land
= length of the other 2 sides of the land
Therefore, we can create two equations from the given information:
Area of land:
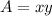
Perimeter of fence:
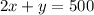
Rearrange the equation for the perimeter of the fence to make y the subject:
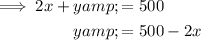
Substitute this into the equation for Area:
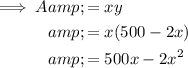
To find the value of x that will make the area a maximum, differentiate A with respect to x:
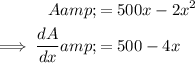
Set it to zero and solve for x:
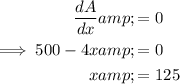
Substitute the found value of x into the original equation for the perimeter and solve for y:
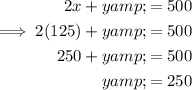
Therefore, the dimensions that will give Christine the maximum area are:
125 m x 250 m (where 250 m is the side opposite the river)
The maximum area is: