Answer:
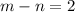
Explanation:
Instead of using the standard form, we can use the vertex form of a quadratic equation:
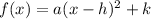
Where a is the leading coefficient, and (h, k) is our vertex.
Our vertex point is at (2, -4). So, let’s substitute 2 for h and -4 for k:
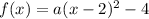
Now, we need to determine a.
We know that it passes through the point (4, 12). So, when x is 4, y must be 12. In other words:

Solve for a. Subtract within the parentheses:
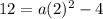
Add 4 to both sides:

Square:

Solve:
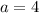
Thererfore, the value of a is 4.
So, our function is:
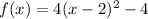
Now, let’s find our roots. Set the equation to 0 and solve for x:
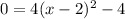
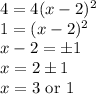
So, our roots are 1 and 3.
The greater root is 3 and the lesser root is 1.
Therefore, m-n, where m>n, is 3-1 or 2.
Our final answer is 2.