Answer:
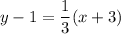
Explanation:
Equation of a Line
The equation of a line passing through points (x1,y1) and (x2,y2) can be found as follows:
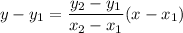
The table shows the relation between x and y. It contains the following points
(-3,1), (6,4), (12,6), (30,12).
Taking the two first points, we find the equation of the line:
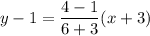
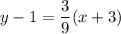
Simplifying:
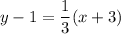
To ensure the rest of the points belong to the line, we test them:
For the point (12,6):
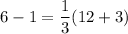
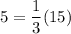
5=5
Since equality is true, the point belongs to the line.
For the point (30,12):
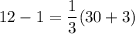
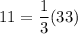
11=11
Since equality is true, the point belongs to the line.
Thus, the equation of the line is:
