Complete Question
The amounts a soft drink machine is designed to dispense for each drink are normally distributed, with a mean of 12.1 fluid ounces and a standard deviation of 0.3 fluid ounce. A drink is randomly selected.
Required:
a) Find the probability that the drink is less than 11.9 fluid ounces
b) Find the probability that the drink is between 11.6 and 11.9 fluid ounces
c) Find the probability that the drink is more than 12.6 fluid ounces. Can this be considered an unusual event? Explain your reasoning.
Answer:
a
![P(X < 11.9 ) = 0.25239 [/tex ] </p><p>b</p><p> [tex]P( 11.6 < X < 11.9 ) = 0.20463](https://img.qammunity.org/2021/formulas/mathematics/college/g5brimyfkg6o057xx40ffi0igs4s9hcn7g.png)
c
![P(X > 12.6 ) = 0.047757 [/tex ] </p><p>Yes It is an unusual event </p><p>Step-by-step explanation:</p><p>From the question we are told that </p><p> The mean is [tex]\mu = 12.1](https://img.qammunity.org/2021/formulas/mathematics/college/2i6g9qka3rfgp9su28eyz9tcxnpwnn8rtc.png)
The standard deviation is
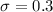
Generally the probability that the drink is less than 11.9 fluid ounces is mathematically represented as
P(X < 11.9 ) = P(\frac{X -\mu}{\sigma } < \frac{11.9 - 12.1}{0.3} )
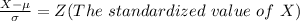
![P(X < 11.9 ) = P(Z< -0.667 ) [/tex ]</p><p>From the z table the area under the normal curve to the left corresponding to -0.667 is </p><p> P(Z< -0.667 ) = 0.25239</p><p>So </p><p> [tex] P(X < 11.9 ) = 0.25239 [/tex ] </p><p> Generally the probability that the drink is between 11.6 and 11.9 fluid ounces is mathematically represented as </p><p>[tex] P( 11.6 < X < 11.9 ) = P( (11.6 -12.1)/(0.3) < (X -\mu)/(\sigma ) < (11.9 - 12.1)/(0.3) )]()
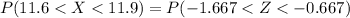
=>
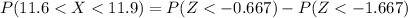
From the z table the area under the normal curve to the left corresponding to -1.667 is
P(Z< -1.667 ) = 0.047757
So
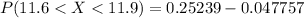
=>
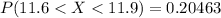
Generally the probability that the drink is more than 12.6 fluid ounces is mathematically represented as
P(X > 12.6 ) = P(\frac{X -\mu}{\sigma } > \frac{12.6 - 12.1}{0.3} )
[tex] P(X >12.6 ) = P(Z> 1.667 ) [/tex ]
From the z table the area under the normal curve to the right corresponding to 1.667 is
P(Z> 1.667 ) = 0.047757
So
[tex] P(X > 12.6 ) = 0.047757 [/tex ]
Given that this probability is less than 0.05 , it mean it is an unusual event