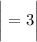Answer:
x = = -5 ; y = -1 ; z = 4
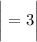
Explanation:
The equation of the plane through (1,-4,0) is,
a(x-1) + b(y+4) + c(z+0) = 0 ....... (1)
Again the plane is perpendicular to the vector (5,1,-4)
So, the direction ratios of the normal to the plane is proportional to the direction ratios of the vector (5,1,-4)
So, a/(5) = b/(1) = c/(-4 )
Let,a/(5) = b/(1) = c/(-4 ) = k
So, a = 5k, b = k and c = -4k
So, from (1) we have,
(5k)(x-1) + (k)(y+4) + (-4k)(z+0) = 0
Thus;
-5(x-1) -(y+4) +4(z+0) = 0
So,
-5x +1 -y-4+4z+0 =0
-5x - y +4z -3 = 0
-5x - y +4z = 3
x = = -5 ; y = -1 ; z = 4