Answer:
The total mass in the tank = 0.45524 kg
The amount of heat transferred = 3426.33 kJ
Step-by-step explanation:
Given that:
The volume of the tank V = 0.06 m³
The pressure of the liquid and the vapor of H2O (p) = 15 bar
The initial quality of the mixture
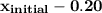
By applying the energy rate balance equation;
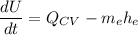
where;
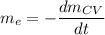
Thus,
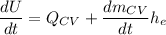
If we integrate both sides; we have:
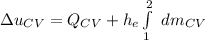
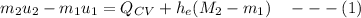
We obtain the following data from the saturated water pressure tables, at p = 15 bar.
Since:
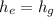
Then:
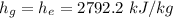
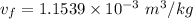
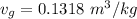
Hence;
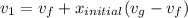
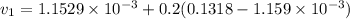
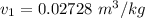
Similarly; we obtained the data for
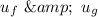 from water pressure tables at p = 15 bar
from water pressure tables at p = 15 bar

Hence;
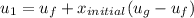
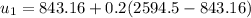
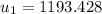
However; the initial mass
 can be calculated by using the formula:
can be calculated by using the formula:
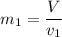
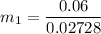
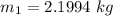
From the question, given that the final quality;
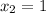
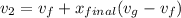

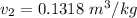
Also;
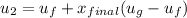
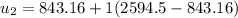
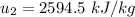
Then the final mass can be calculated by using the formula:
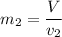

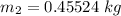
Thus; the total mass in the tank = 0.45524 kg
FInally; from the previous equation (1) above:
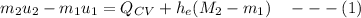
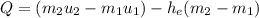
Q = [(0.45524)(2594.5) -(2.1994)(1193.428)-(2792.2)(0.45524-2.1994)]
Q = [ 1181.12018 - 2624.825543 - (2792.2)(-1.74416 )]
Q = 3426.33 kJ
Thus, the amount of heat transferred = 3426.33 kJ