Answer:
The probability that the person answered "yes" or was male is 0.537
Explanation:
The union of events is equivalent to the disjunction "or". Given two events A and B, the union of events, denoted by A∪B, is defined as the event formed by all the elements that are in A or B. That is, the event A∪B is verified when one of the two or both occurs.
Considering two events A and B with probabilities P (A) and P (B), respectively, the probability of their union is given by:
P(A∪B)= P(A) + P(B) - P(A∩B)
In this case:
- A: the person answered "yes"
- B: the person was male
So, being the probability calculated as the number of favorable cases divided by the total number of possible cases, then in this case it is known that the number of people who answered yes is 64, while the number of people who responded is not 70. Therefore , the total number of people who answered is equal to 64 + 70 = 134. So, the probability of answering yes is:
P(A)=
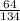=0.478
On the other hand, you know that out of 64 people who answered yes, the number of being male is 6. And out of 70 people who answered no, the number of being male is 8. So the probability that men answer yes is calculated as:
P (A∩B) =
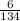= 0.045
Finally, with the total number of men equal to 6 + 8 = 14, the probability of being male is:
P(B)=
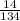= 0.104
Then:
P(A∪B)= P(A) + P(B) - P(A∩B)
P(A∪B)= 0.478 + 0.104 - 0.045
Solving:
P(A∪B)= 0.537
The probability that the person answered "yes" or was male is 0.537