1 Answer

Gotgenes · Answer 1 · 2021-02-13T07:17:05+0000

Answer:

The solution of this differential system is
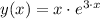$y(x) = x\cdot e^(3\cdot x)$ .

Explanation:

This second-order differential equation is homogeneous and linear of the form:

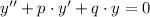$y'' + p\cdot y' +q\cdot y = 0$ (1)

Where:

- First-order constant coefficient, dimensionless.

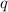- Zero-order constant coefficient, dimensionless.

Whose characteristic polynomial is:

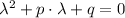$\lambda^(2)+p\cdot \lambda + q = 0$ (2)

Where
$\lambda$ contains the roots associated with the solution of the differential equation.

If we know that
p = 6 and
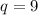q = 9 , the roots of the characteristic equation are, respectively:

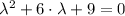
$\lambda^(2)+6\cdot \lambda + 9 = 0$

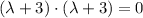
$(\lambda +3)\cdot (\lambda + 3) = 0$

Which means that
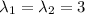$\lambda_(1) = \lambda_(2) = 3$ and the solution of the differential equation is of the form:

$y(x) = e^(3\cdot x)\cdot (c_(1)+c_(2)\cdot x)$ (3)

Where
c_(1) and
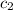c_(2) are integration constants.

The first derivative of the equation above is:

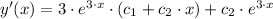$y'(x) = 3\cdot e^(3\cdot x)\cdot (c_(1)+c_(2)\cdot x)+c_(2)\cdot e^(3\cdot x)$ (4)

Now, if we get that
y(0) = 0 and
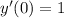y'(0) = 1 , then the system of equations to the solved is:

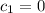c_(1) = 0 (3b)

c_(1)+c_(2) = 1 (4b)

The solution of this system is:
c_(1) = 0 ,
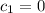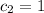c_(2) = 1 . Therefore, the solution of this differential system is
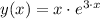$y(x) = x\cdot e^(3\cdot x)$ .

Please log in or register to add a comment.