Answer:
(1,1) and (7,5) => Slope: 2/3
(1,1) and (5,7) => Slope: 3/2
(2,5) and (-1,2) => Slope:1
(2,5) and (-7,-4) => Slope:1
Explanation:
The slope of a line is denoted by m and is given as:
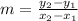
Calculating the slope one by one for each pair.
(1,1) and (7,5):
Let m1 be the slope of this line
Here
(x1,y1) = (1,1)
(x2,y2) = (7,5)
Putting values in formula
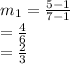
(1,1) and (5,7):
Let m2 be the slope of this line
Here
(x1,y1) = (1,1)
(x2,y2) = (5,7)
Putting values in formula
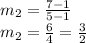
(2,5) and (-1,2):
Let m3 be the slope of this line
Here
(x1,y1) = (2,5)
(x2,y2) = (-1,2)
Putting values in formula

(2,5) and (-7,-4):
Let m4 be the slope of this line
Here
(x1,y1) = (2,5)
(x2,y2) = (-7,-4)
Putting values in formula
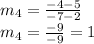
Hence,
The points and their respective slopes are as follows:
(1,1) and (7,5) => Slope: 2/3
(1,1) and (5,7) => Slope: 3/2
(2,5) and (-1,2) => Slope:1
(2,5) and (-7,-4) => Slope:1