Answer: 36pi (choice b)
===========================================================
Step-by-step explanation:
Let x = length of side BC
This is the height of the cylinder. Think of a can that is laying on its side. The radius of this can or cylinder is CD
If point B has x coordinate of 12, and BC is 12 units long, this must mean point C has x coordinate of 12-x. This is plugged into the function to show that CD has a length of exactly
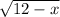
This is the radius of the cylinder
The volume of a cylinder is

Plug in the radius and height mentioned to get this function in terms of x
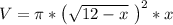
That simplifies to
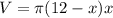
or
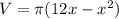
Ignore the pi portion for now.
We wish to maximize the function f(x) = 12x-x^2
Use either calculus (specifically derivatives) or a graphing calculator to find that the vertex is at (6, 36)
This means x = 6 leads to the largest f(x) value being 36.
Therefore, the volume V is maxed out when x = 6 and we get a max volume of 36pi cubic units.