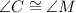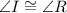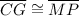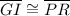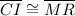Answer:
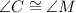

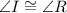
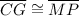
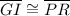
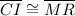
Explanation:
Given the congruence statement ∆CGI
 ∆MPR, it follows that the corresponding sides of both ∆s are equal, as well as the corresponding vertices or angles. It implies that ∆CGI and ∆MPR are of the same shape and size.
∆MPR, it follows that the corresponding sides of both ∆s are equal, as well as the corresponding vertices or angles. It implies that ∆CGI and ∆MPR are of the same shape and size.
✅Thus, the 6 pairs of the corresponding congruent parts of ∆CGI and ∆MPR are: