If hose A takes x hours to fill the pool, hose B will take x+3 hours to fill the pool. So, each hour, A will fill
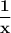 parts of the pool and B will fill
parts of the pool and B will fill
 parts. Since using both hoses fills the pool completely, you have to:
parts. Since using both hoses fills the pool completely, you have to:
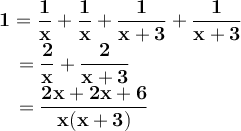
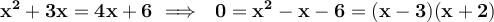
Hose A takes 3 hours to fill the pool and Hose B takes 6 hours.